A frequency polygon graph is a widely used statistical tool that converts raw data into a simple visual form. It is created by connecting the midpoints of class intervals with straight lines, resulting in a polygonal shape that highlights data distribution patterns. This graphical method makes it easy to identify peaks, trends, and variations in large data sets.
The construction of a frequency polygon is straightforward, yet it provides powerful insights. Students, researchers, and professionals often use it to compare multiple distributions, analyze trends, and present statistical information in an effective and easy-to-understand format.
frequency polygon in statistics
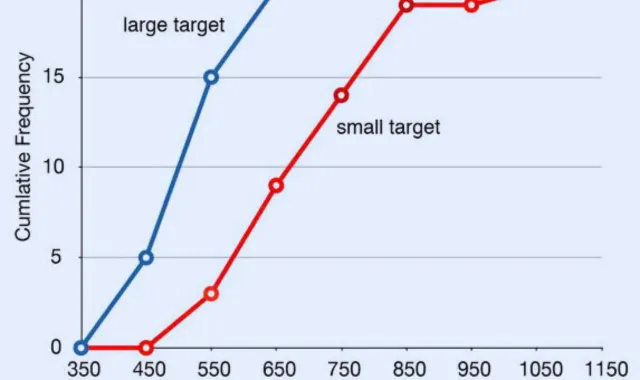
A frequency’s polygon in statistics is a graphical method of representing data distribution by joining the midpoints of class intervals with straight lines. It provides a clear picture of how frequencies are spread across different ranges. Widely used in statistical studies, it helps in comparing data sets, analyzing trends, and simplifying large numerical information.
Frequency Polygon at a Glance
| Feature | Description |
| Definition | A graph showing frequency distribution using straight-line segments |
| Construction Basis | Midpoints of class intervals connected with straight lines |
| Formula Involved | Frequency plotted against class midpoints |
| Common Uses | Comparison of multiple data sets, trend analysis, and data distribution |
| Advantage | Simpler than histograms, easy to interpret visually |
What is a Frequency Polygon?
A frequency polygon is a type of line graph that depicts the frequencies of different intervals of data. Unlike a histogram, which uses bars, a frequency polygon uses straight-line segments connected through plotted points at the midpoint of each interval.
This makes the graph more refined and easier to compare with other data sets. In essence, it provides a bird’s-eye view of how data values are distributed across intervals and whether the pattern is skewed, symmetric, or follows a particular trend.
histogram and frequency polygon
A histogram and a frequency’s polygon are both tools for representing frequency distributions in statistics. A histogram uses adjacent bars to show frequencies of class intervals, while a frequency’s polygon connects class midpoints with straight lines. Both highlight data patterns, but polygons allow easy comparison of multiple distributions, whereas histograms are more detailed for individual data sets.
Construction of a Frequency Polygon
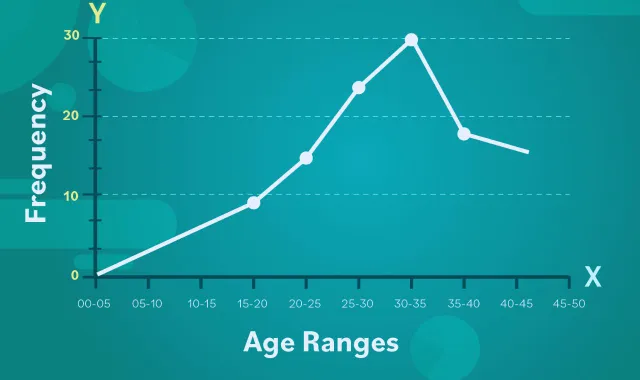
The construction of a frequency’s polygon follows a systematic process. Below are the steps:
Step 1: Prepare the Frequency Table
Collect the raw data and organize it into a frequency distribution table, including class intervals, frequencies, and midpoints.
Step 2: Find the Class Midpoints
The midpoint of each class interval is calculated using
Midpoint = Lower Class Limit + Upper Class Limit 2\ text{Midpoint} = \frac{\ text{Lower Class Limit + Upper Class Limit}} {2} Midpoint=2 Lower Class Limit + Upper Class Limit
Step 3: Plot the Points
On a graph, plot the midpoints of the class intervals on the X-axis and their respective frequencies on the Y-axis.
Step 4: Connect the Points
Join the plotted points using straight lines to form a polygon. For closure, connect the polygon to the X-axis at both ends, usually at zero frequency.
Step 5: Label and Interpret
Finally, label the axes and provide a suitable title. Interpretation of the polygon depends on the shape, peaks, and spread of the distribution.
Formula of Frequency Polygon
While there isn’t a single rigid formula, the foundation of a frequency’s polygon lies in plotting frequency (f) against class midpoint (x).
Mathematically, it can be expressed as
P(x)=fat at each midpoint of the interval P(x) = f \quad \text{at each midpoint of the interval} P(x)=fat at each midpoint of the interval
Where:
- xxx = class midpoint
- fff = frequency of that class
Thus, the points (x,f)(x,f)(x,f) are plotted and joined to form the polygon.
Example of Frequency Polygon Construction
Suppose the following data shows the number of students scoring within certain mark ranges in an exam:
- 0–10: 5 students
- 10–20: 8 students
- 20–30: 12 students
- 30–40: 15 students
- 40–50: 10 students
Step 1: Calculate Midpoints
- 5, 15, 25, 35, 45
Step 2: Plot Points
- (5, 5), (15, 8), (25, 12), (35, 15), (45, 10)
Step 3: Connect
Join these points with straight lines and extend to the X-axis at 0 frequency before the first and after the last midpoint. The resulting graph is a clear frequency’s polygon.
frequency polygon example
A frequency’s polygon example can be seen in student exam scores. Suppose marks are grouped into intervals like 0–10, 10–20, 20–30, and so on. By calculating midpoints (5, 15, 25, etc.) and plotting them against their frequencies, the points are joined with straight lines, forming a polygon. This clearly shows performance trends across score ranges.
Uses of Frequency Polygon
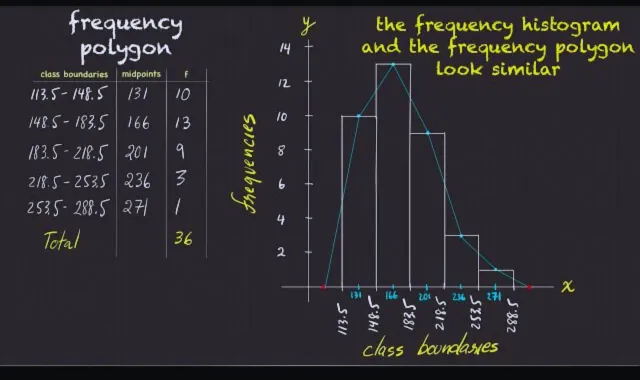
Frequency’s polygons are widely used across multiple fields due to their simplicity and effectiveness.
- Comparison of Data Sets: Frequency’s polygons allow easy comparison between two or more data sets by plotting them on the same graph. This makes it simple to identify differences or similarities in distribution.
- Trend Analysis: They help analyze the overall shape of data, revealing skewness, central tendency, and variation in distribution.
- Simplification of Large Data: By condensing large data sets into a simple polygon, frequency polygons make complex numbers digestible.
- Statistical Studies: Researchers and analysts rely on frequency’s polygons in descriptive statistics, probability studies, and graphical representations of survey data.
- Educational Use: Students learn data handling through frequency’s polygons, as it bridges the gap between numerical calculations and visual interpretation.
Advantages of Frequency Polygon
- Easy to draw and interpret.
- Useful for comparing multiple distributions in one graph.
- Requires less space compared to histograms.
- Highlights the overall shape of the distribution effectively. Easy to draw and interpret.
- Useful for comparing multiple distributions in one graph.
- Requires less space compared to histograms.
- Highlights the overall shape of the distribution effectively.
Limitations of the Frequency Polygon
- Less precise than histograms for detailed frequency distribution.
- Requires accurate calculation of midpoints.
- Not suitable for very small data sets.
- Loses clarity if too many class intervals are included.
histogram frequency polygon
A histogram frequency’s polygon combines two graphical methods to represent data. The histogram displays frequencies with bars for each class interval, while the frequency’s polygon overlays straight lines connecting midpoints of these intervals. Using both together enhances clarity, showing distribution patterns and allowing comparisons, making it an effective approach in statistics for data analysis and interpretation.
Difference between histogram and frequency polygon
Although frequency’s polygons and histograms are closely related, they differ significantly in representation:
- Histogram: Uses bars for each class interval.
- Frequency’s Polygon: Uses straight-line segments connected at midpoints.
- Comparison: Frequency’s polygons allow multiple data sets on the same graph, unlike histograms.
frequency polygon example problems
Frequency’s polygon example problems often involve constructing graphs from grouped data. For instance, if the marks of students are grouped into intervals like 0–10, 10–20, 20–30, etc., you first calculate the midpoints, then plot them against frequencies. Connecting these points forms the polygon, helping analyze score distribution, trends, and comparisons between different data sets effectively.
frequency polygon class 9
A frequency polygon, Class 9, is part of the statistics syllabus where students learn to represent data graphically. It is created by plotting frequencies against class midpoints and joining the points with straight lines. This method helps students visually interpret data distribution, compare sets, and understand trends, making it an essential concept in basic statistics education.
Real-Life Applications of Frequency Polygon
- Business: Sales data analysis over months or years.
- Education: Student performance distribution.
- Health: Tracking patient data, such as age distribution.
- Market Research: Consumer behavior analysis.
- Government Statistics: Population studies, income distribution, etc.
FAQs on Frequency Polygon
Q1. What is a frequency polygon in simple terms?
Ans: A frequency polygon is a graph that shows data distribution using straight lines connecting midpoints of class intervals, making it easy to visualize trends.
Q2. How is a frequency polygon constructed?
Ans: It is constructed by plotting frequencies against class midpoints and joining these points with straight lines. The graph is closed at both ends by touching the X-axis.
Q3. Why is a frequency polygon useful?
Ans: It simplifies large data sets, makes comparisons easier, and helps identify patterns and trends in distribution.
Q4. Can we draw a frequency polygon without a histogram?
Ans: Yes, it can be drawn directly from the frequency table by calculating midpoints and plotting them with frequencies. A histogram is not mandatory.
Q5. What is the difference between a histogram and a frequency polygon?
Ans: A histogram uses bars to represent frequencies, while a frequency polygon uses connected straight lines at midpoints. Polygons are more effective for comparing multiple distributions.
Q6. How to draw a frequency polygon?
Ans: To draw a frequency polygon, prepare a frequency table, calculate class midpoints, plot midpoints against their frequencies on a graph, and join the points with straight lines. Finally, close the polygon by connecting it to the X-axis.
Q7. How to make a frequency polygon?
Ans: To make a frequency polygon, organize data into a frequency table, find the midpoints of class intervals, plot frequencies against these midpoints, and join the points with straight lines. Close the shape by connecting the ends to the baseline.
Final Thoughts
Frequency polygons are vital in statistical analysis, as they transform complex numbers into simple visual patterns. By connecting class midpoints with straight lines, they make trends, peaks, and comparisons easy to identify, enhancing data interpretation for students, researchers, and professionals.
Mastering the construction and uses of frequency polygons not only strengthens statistical understanding but also improves data presentation. Their clarity, adaptability, and practical relevance ensure they remain a trusted tool in classrooms, research, and business analysis.